This is a project I worked on recently with my good friend James Boyce. Born out of a tool he’d been using with workmates, an open-source, very barebones version of Donut

You can see the code and try it yourself here: https://github.com/B0yc3y/doughnut

What does it do? It’s a Slack bot that helps bring together teams working remotely, giving a bit of the water-cooler / going-out-for-coffee feel that you don’t get when everyone is working from home. Every two weeks, it pairs up users in a Slack channel and encourages them to set up time for a one-on-one meeting, to have a coffee and chit-chat.

I started helping James out with the bot as a fun lockdown project. When I first saw the bot it worked, but it was extremely slow to build and to run.

Doughnut was originally written by some data scientists in James' team, who used Pandas and made everything Dataframes

Now Pandas is a great library, with some powerful and useful tools for data analysis. And Dataframes are a very flexible tool that lets you write SQL-like operations on 2D datasets, which is handy. But it’s huge overkill for what we want to do:

1. Get a list of users
2. For each pair of users, calculate a “score” for the match
3. Choose pairs so that everyone is selected, in a way that attempts to maximise total score

This can all be done with simple lists, dicts and sets.

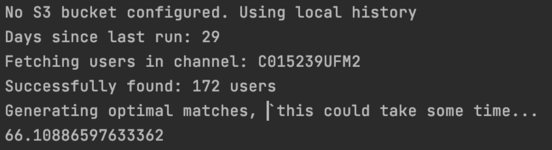
By doing away with the Pandas dependency, and improving some nested loops and other inefficient code, I managed to bring the runtime channel of 172 users down from 66 seconds to 37ms, an 1800x improvement!

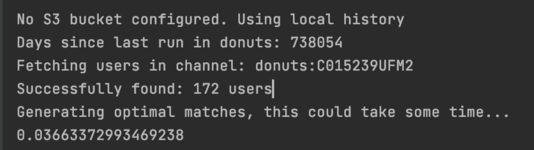
This also means we can use an Alpine base image rather than Debian, which brings the size of the docker image down from 1.2 GB to 120 MB. This gives a much faster image build time, and a much faster image pull and startup time in fargate.

The data structure

We store a complete history of matches as a CSV. CSV was chosen mostly for human readability, and the ability to import it into spreadsheet programs etc for calculating statistics if desired.

name1, name2, conversation_id, match_date, prompted
alice, bob, A123456789, 2021-08-31, 1
bob, charlie,, B123456789, 2021-09-14, 0

This is parsed into a list of dicts, which is iterated over to count matches:

[
    {"name1": "alice", "name2": "bob", "conversation_id": "A1234567", "match_date": "2021-08-31", "prompted": "1"},
    {"name1": "bob", "name2": "charlie", "conversation_id": "B1234567", "match_date": "2021-09-14", "prompted": "0"}
]

{
    'Alice': {
        'Bob': ['2021-08-31']
    },
    'Bob' :{
        'Alice': ['2021-08-31'],
        'Charlie': ['2021-09-14']
    }
}

Currently that means that we have to recount the times that each pairing has met, every time we run the program. A future improvement would be to store the match count for pairs, to avoid recalculation.

The algorithm

Matching up users in an optimal fashion turns out to be a difficult problem.

You can think of it as a graph problem. We have a complete graph where each person is a node, and each match is an edge. Then we have a weighting for each edge that is how “good” the match is.

We want to get a set of edges, so that each node is represented in one and only one edge, and so that the total weight of edges is maximised. This is a Maximum Weight Matching problem. In the above graph, the maximm solution would be to to match Alice with Dave, and Bob with Charlie, to get a total score of 3.0 + 4.3 = 7.3.

There are many lengthy mathematics papers written on solutions for this problem. One example solution is the Hungarian Algorithm, which is O(N^3) where N is the number of vertices/nodes/users.

A good compromise is just to make a greedy algorithm. Pick the pair (edge) with the highest score, remove those two users (nodes), and repeat. This requires the list of matches to be sorted by score. Since the list has N^2 items, the expected complexity is O(N^2*log(N^2)).

With the above graph, this would first pick the pair of Charlie and Dave (5.0), which leaves Alice matched with Bob. This isn’t particularly optimal, as the Alice-Bob match is pretty low scoring. But as the graph gets larger, I’d expect the greedy algorithm to get better and have a small proportion of very-bad matches.

Match score calculation

How do you decide how good a pairing is? Its a debateable question, and there are a lot of factors that you could involve. At the moment, the calculation is really simple - it just involves how often the two users have met before, and whether they are in a different timezone or not. This means (theoretically) that you should be matched with everyone else once before you match with someone a second time.

For ease of extension, the match strength calculation is extracted into a separate function which makes changing the scoring rules easy.

Talking to Slack

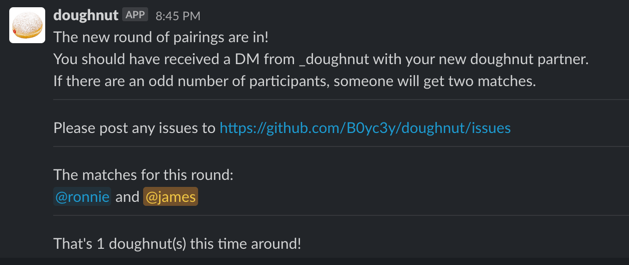
Once a Slack app is created for your workspace (a good tutorial here), and given appropriate permissions, the application uses the Slack Python SDK to create DMs for each matched pair, and post a list of matches to the group channel.

Running automatically

Because the python application can be bundled into a small docker image, it is simple to set up as a Fargate task. A scheduled event in EventBridge can trigger the task at regular intervals.